1. 대칭 키 암호 알고리즘
1. 일반적인 개념
1. 용어정리
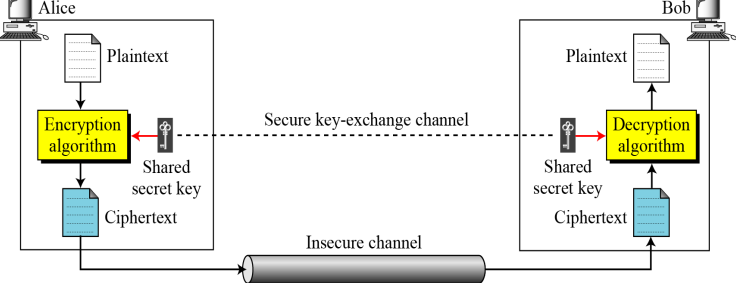
암호화(Encryption): 평문을 암호문으로 변환하는 과정
복호화(Decryption): 암호문을 평문으로 변환하는 과정
평문(plaintext): Alice가 BOb에서 보낼려는 메시지 원본
암호문(ciphertext): 평문을 암호화한 후 채널을 통해 실제 저송하는 메시지
암호 알고리즘(encryption algorithm):암호화를 하는 방법
키(key): 암호가 동작하는데 필요한 값들의 집합
비밀키(secret key): 암호알고리즘을 통화 암호화를 할 때 필요한 키
복호 알고리즘(decryption algorithm): 복호화를 하는 방법
2. 대칭키 암호의 일반적인 알고리즘
0. 가정: 공격자가 도청하여 메시지 내용을 알아낼 수 없음&
Alice와 Bob은 안전하지 않은 채널(insecure channel)을 통해 메시지를 전송함.&
Alice와 Bob은 같은 암호기를 공유함.
1. Alice는 비밀키, 암호 알고리즘을 통해 평문을 암호문으로 바꾼다.
2. Alice는 안전하지 않은 채널을 통해 Bob에게 암호문을 전달.
3. Bob은 비밀키와 복호화 알고리즘을 통해 암호문을 평문으로 바꾼다.
n명의 그룹을 위한 대칭 키는 n(n-1)/2 (n명중 2명을 뽑는 경우의 수)개의 키가 필요하다.
2. 수학적 표현
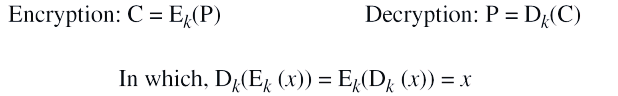
P: palintext(평문)
C: ciphertext(암호문)
함수E: encryption(암호화)
함수D: decryption(복호화)
2. 케르크호프스의 원리(kerckhoff's principle)
1. 암호체계는 수학적으로는 해독불가능하지 않다고 하더라도, 실질적으로 그래야한다.
2. 암호체계는 비밀에 부쳐질 필요가 없어야만 하며, 적의 손에 떨어지더라도 문제가 없어야 한다.
3. 키는 글로 쓰여지지 않더라도 교환 혹은 보관할 수 있어야 한다. 당사자들의 의지에 의해서 바뀌거나 수정될 수 있어야 한다.
4. 전신에 적용할 수 있어야 한다.
5. 이동이 가능해야하며, 암호 체계의 사용과 기능을 위해 여러 사람의 협력을 필요로 하지 않아야 한다.
6. 마지막으로, 시스템의 활용을 요구하는 여러 상황들이 주어졌을 때, 암호 체계는 이용이 쉬워야 하며, 정신적인 압박감이나 여러 규칙들의 관찰을 필요로 하지 않아야 한다.
몇가지 항목들은 복잡한 암호화를 수행할 수 있는 컴퓨터의 존재로 인해 더이상 의미가 없어졌지만, 2번째 항목은 이제 케르크호프스의 원리로 알려지게 되었으며(무인 무기 등), 아직까지도 매우 중요한 의미를 가지고 있다.
간단하게 말해, 암호체계의 안전성은 키의 비밀성에만 의존해야한다
3. 암호 해독 공격(cryptanalysis attack)

암호문 단독 공격(전수조사 공격, 통계적인 공격, 패턴 공격): 공격자가 암호문만 알고 있을 때 할 수 있는 공격하는 유형.
알고있는 평문 공격: 공격자가 일정 부분의 평문과 이에 대응하는 암호문을 가진 상태에서 공격하는 유형
선택 평문 공격: 공격자가 많은 수의 평문을 암호문으로 만들 수 있는 상태에서 공격하는 유형. 하지만 공격자는 암호화 알고리즘이나 암호키에 대한 정보는 모르고 있는 상태
선택 암호문 공격: 공격자가 많은 수의 암호문에 대해 평문으로 가지고 있는 상태에서 공격하는 유형.공격자는 암호키에 대한 정보는 모르는 상태.
https://johyungen.tistory.com/389
암호 공격(암호문 단독, 알려진 평문, 선택 평문, 선택 암호문)
1. 암호문 단독 공격 (Ciphertext-Only Attack) 공격자가 암호문만 가지고 있는 상황에서 공격하는 유형, 공격자는 암호문 이외의 어떤 정보도 가지고 있지 않기 때문에 공격자 입장에
johyungen.tistory.com
4. 대치 암호(substitution ciphers)
대치암호: 하나의 기호(symbol)를 다른 기호로 변경하여 암호화한다.
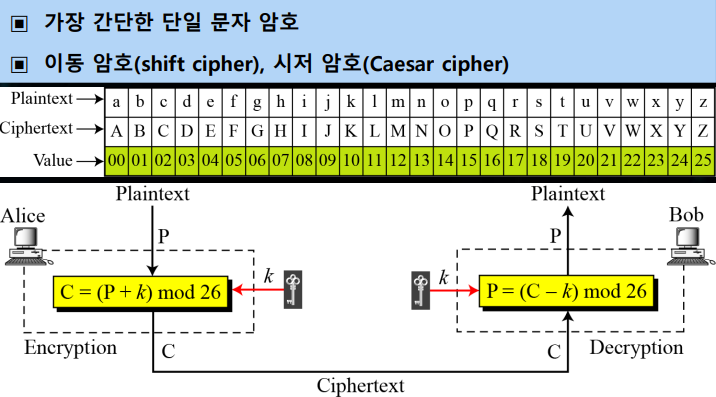
1. 단일문자 암호(Monoalphabetic Ciphres)
1, 덧셈암호
2. 곱셈암호

Zn: Z보다 작은 정수의 집합
Zn*: Z보다 작으면서, Z와 서로소인 정수를 갖는 집합(1은 포함)
더 자세한 건 아래글 키 공간 참조
2022.10.10 - [분류 전체보기] - [암호학] 2장 정리(2). 모듈로 연산과 일변수 선형 방정식
[암호학] 2장 정리(2). 모듈로 연산과 일변수 선형 방정식
잉여집합(set of residues) : 모듈로 연산 즉, a mod n의 결과값은 항상 0과 n-1사이의 정수이다. --> 정수에서의 연산을 항상 닫혀있는 연산으로 할 수 있다. 잉여류(Residue Classes) : 모듈로 n에 함동인 정수
sh1256.tistory.com
3. 아핀암호
덧셈암호와 곱셈암호를 함께 사용한다.


문제점
--> 덧셈암호, 곱셈암호에 비해서는 더 큰 키 공간을 갖는다.
하지만 컴퓨터가 발달함에 따라 아핀암호의 키 공간도 전수조사 공격에 취약하게 되었다.
해결 방법
평문 문자와 대응하는 암호문 문자 사이의 사상(mappting)을 구성하기.
'보안 공부 > 암호학' 카테고리의 다른 글
| [암호학] 전치암호과 대치암호의 비교 & 확산과 혼돈 (0) | 2022.10.12 |
|---|---|
| [암호학] 3장 정리(2). 단일 문자 대치 암호, 다중 문자 대치 암호의 예시 (0) | 2022.10.11 |
| [암호학] 2장 정리(2). 모듈로 연산과 일변수 선형 방정식 (0) | 2022.10.10 |
| [암호학] 2장 정리(1). 암호학의 개념과 암호수학 (0) | 2022.10.10 |
| [암호수학1] 유클리드 알고리즘 + 디오판투스 방정식 (특수해와 일반해 구하기) (1) | 2022.09.21 |