728x90
[암호수학1] 유클리드 알고리즘 이론~코딩
유클리드 알고리즘(Euclidean algorithm)이란? 유클리드 알고리즘(유클리드 호제법)은 자연수 2개의 최대공약수를 구하는 하나의 알고리즘이다. 유클리드 알고리즘을 쓰면, a와 b의 공약수들을 나열하
sh1256.tistory.com
위 게시물(유클리드 알고리즘 (+확장))을 먼저 보고 오셔야 이해가 됩니다.
자 그럼 ax+by=c 중 (x,y)가 무수하게 많아지는 경우가 있습니다.
아래 예재의 10x + 5y=30만 봐도 쉽게 알 수 있죠.
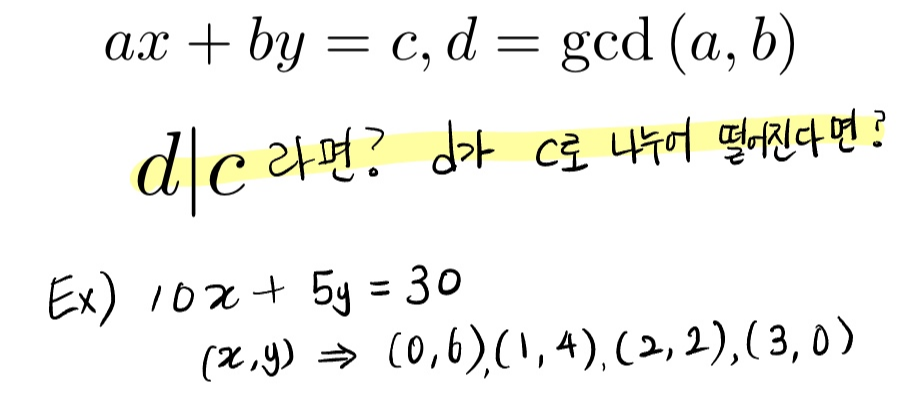
컴퓨터는 이렇게 많은 (x,y)쌍 중 하나를 골라서 사용해야 합니다. 여러개를 혼용해서 사용하면 에러가 뜨로 혼동이 오니까요. 여러개의 (x,y) 중 특수해(Particular solution)를 아래와 같이 정의합니다.
이 때 d = gcd(a,b)
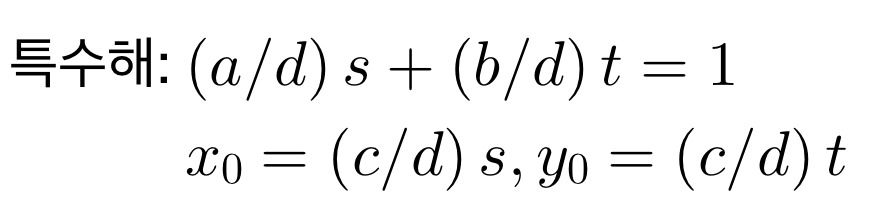
이렇게 수식으로 보니까 헷갈립니다.

예시를 하나 들어서 설명하겠습니다.

[특수해 구하기]
자 그럼 먼저 특수해를 구할 수 있는 식으로 바꿔봅시다.
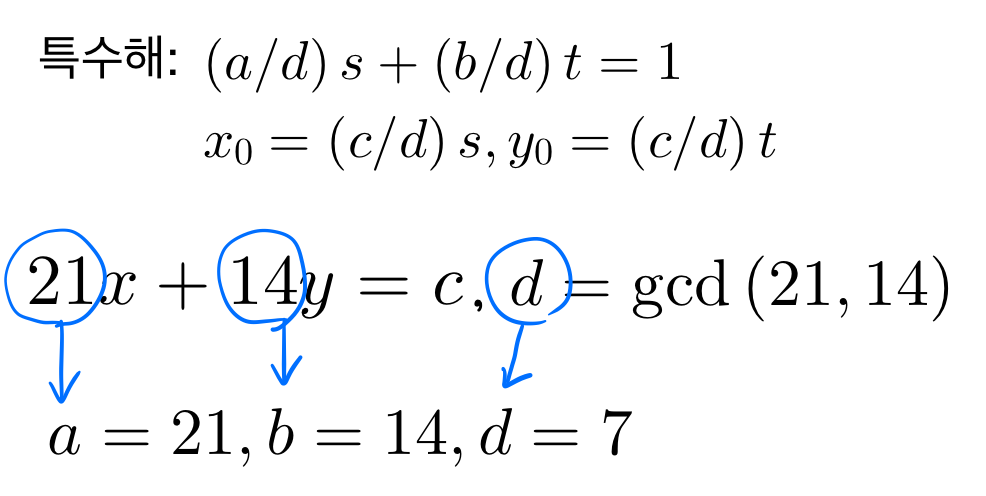
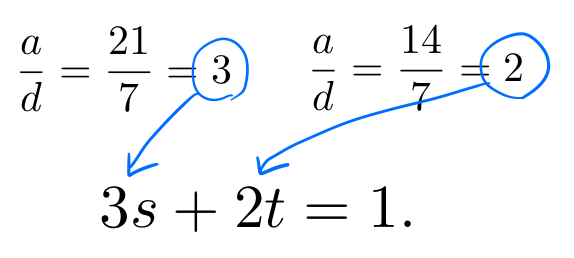
이 때 3과 2의 최대공약수가 1이 됩니다. gcd(3,2)=1.
그러면 유클리드 확장 알고리즘을 사용할 수 있겠죠?
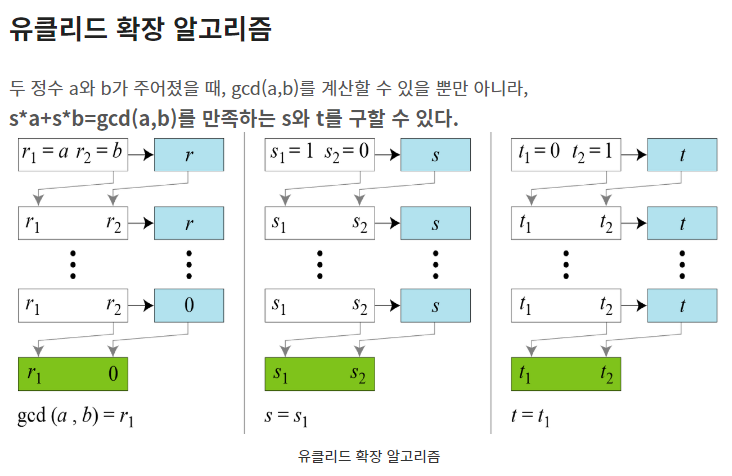
저는 이전 계시물에서 작성했던 코드를 사용해 s와 t 값을 구했습니다.

코드 실행 결과 s=1, t=-1을 구했습니다.
그러면 결과적으로
21x+14y=35의 특수해는
[x=(c/d)*s=5, y=(c/d)*t=-5]
(5,-5)인 것입니다.
[일반해 구하기]
일반해는 아래와 같이 구할 수 있습니다. 이 때 x0과 y0은 각각 특수해*(c/d)를 나타냅니다.
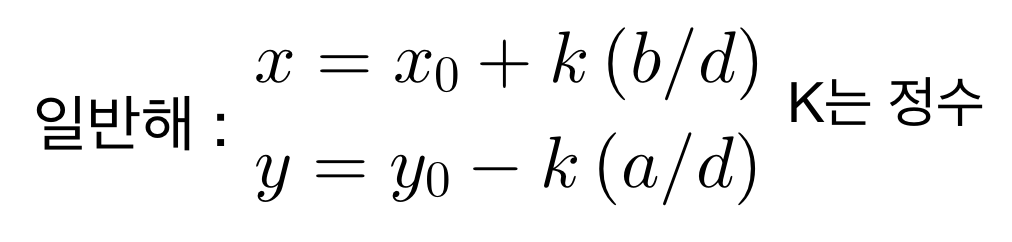
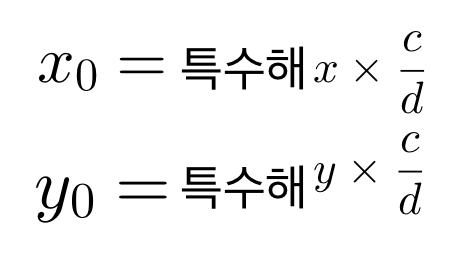
그럼 21x+14y=35에 맞게 식을 채워볼까요? d는 여기서도 a와 b의 최대공약수입니다.

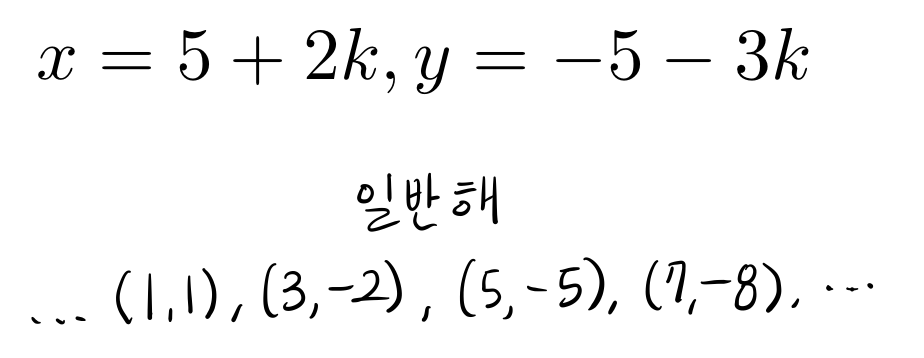
아래는 특수해와 일반해를 구하는 예시를 정리해 놓은 것

'보안 공부 > 암호학' 카테고리의 다른 글
| [암호학] 2장 정리(2). 모듈로 연산과 일변수 선형 방정식 (0) | 2022.10.10 |
|---|---|
| [암호학] 2장 정리(1). 암호학의 개념과 암호수학 (0) | 2022.10.10 |
| [암호수학1] 유클리드 알고리즘 이론~코딩 (0) | 2022.09.18 |
| [암호학] 1장 정리. 현대암호 이론 기본정리 (0) | 2022.09.18 |
| 패딩과 운영모드 (0) | 2022.01.25 |